If we want to distribute the mathematical processing of a matrix multiplication we need an algorithm that can be split and performed in parallel. Looking at the algorithm I alluded to in the last article, I think I can see how to do that. Here’s my thinking.

To multiple a Matrix M with a Vector f use the top equation.

The second equation is for a single element in the solution vector g.

The third equation is a rewrite of the second equation broken into two stages. I have explicitly made these sub-functions of size 4, although the approach should be generalizable.

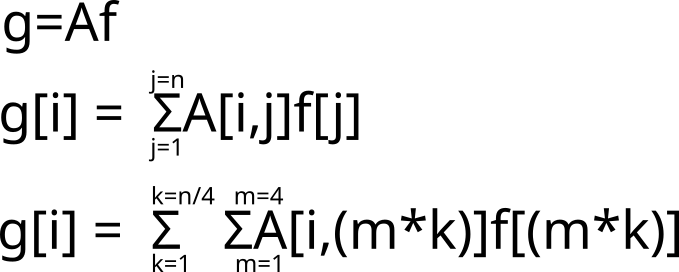
in code

int DIM = 4;

for (int i = 0; i < DIM; i++){
    g[i] = 0;
    for int (j = 0; j < DIM; j++){
        g[i] = g[i] + M[i][j] * f[i];
    }
}
What should be clear is that the body of the outer loop could be executed in parallel.  However, that still has us working on a complete vectors worth of math at a time, and we are going to want to chunk up that vector.
Lets use n as to mean the number of elements in the vector, which is also the number of elements in one dimension of the matrix.

int DIM = 4;

int n = 2;

for (int i = 0; i < DIM; i++){
    g[i] = 0;

    for int (k = 0; k < DIM/n; k++){
        for (m=0; m < n; m++){ 
            j = m * k;
            g[i] = g[i] + M[i][j] * f[i];
        }
    }
}

It should be fairly clear that these are performing the same operations. What is different is the mechanism by which the loop counters are incremented.

Lets step through it. I am going to use a 2X2 matrix to start

g[1] = bh + gh

M = [ [a,b][c,d]]    f= [g,h]

DIM = 2

n = 1

i = 0;

g[i] = 0

j =0

// g[i] = 0 + M[i,j] * f[i]   

//       = 0 + M [0,0] = f[0]

g[0] = ag

i=0, j=1

g[0] = ag + bg

i=1

g[1] = 0

i=1; j =0 

g[1] = 0 + bh

i=1; j =1

Thus our final vector = [[ag + bg, bh + gh]]

It should be fairly clear that the only difference between the algorithms should be the increment of the k and m variables and their summation into j.

what we then want to do is to be able to call a function that executes just the innermost loop:

void partial(k, i, g, M, f){ 
        for (m=0; m < n; m++){ 
            j = m * k;
            g[i] = g[i] + M[i][j] * f[i];
        }
}

Or a comparable function that calculates the same values. More on this in an future article.