If we want to distribute the mathematical processing of a matrix multiplication we need an algorithm that can be split and performed in parallel. Looking at the algorithm I alluded to in the last article, I think I can see how to do that. Here’s my thinking.
To multiple a Matrix M with a Vector f use the top equation.
The second equation is for a single element in the solution vector g.
The third equation is a rewrite of the second equation broken into two stages. I have explicitly made these sub-functions of size 4, although the approach should be generalizable.
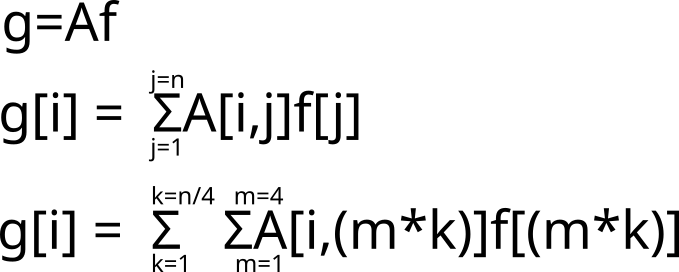
in code
int DIM = 4;
for (int i = 0; i < DIM; i++){
g[i] = 0;
for int (j = 0; j < DIM; j++){
g[i] = g[i] + M[i][j] * f[i];
}
}
What should be clear is that the body of the outer loop could be executed in parallel. However, that still has us working on a complete vectors worth of math at a time, and we are going to want to chunk up that vector.
Lets use n as to mean the number of elements in the vector, which is also the number of elements in one dimension of the matrix.int DIM = 4;
int n = 2;
for (int i = 0; i < DIM; i++){
g[i] = 0;
for int (k = 0; k < DIM/n; k++){
for (m=0; m < n; m++){
j = m * k;
g[i] = g[i] + M[i][j] * f[i];
}
}
}
It should be fairly clear that these are performing the same operations. What is different is the mechanism by which the loop counters are incremented.
Lets step through it. I am going to use a 2X2 matrix to start
g[1] = bh + gh
M = [ [a,b][c,d]] f= [g,h]
DIM = 2
n = 1
i = 0;
g[i] = 0
j =0
// g[i] = 0 + M[i,j] * f[i]
// = 0 + M [0,0] = f[0]
g[0] = ag
i=0, j=1
g[0] = ag + bg
i=1
g[1] = 0
i=1; j =0
g[1] = 0 + bh
i=1; j =1Thus our final vector = [[ag + bg, bh + gh]]
It should be fairly clear that the only difference between the algorithms should be the increment of the k and m variables and their summation into j.
what we then want to do is to be able to call a function that executes just the innermost loop:
void partial(k, i, g, M, f){
for (m=0; m < n; m++){
j = m * k;
g[i] = g[i] + M[i][j] * f[i];
}
}Or a comparable function that calculates the same values. More on this in an future article.
